Lecture Notes on Static Analysis
Lecture Notes on Static Analysis
记录一些学习程序分析的感想
Rice’s theorem
图灵停机问题证明了不存在一个通用的程序,对任意输入的程序P,能判断P会在有限时间内结束。 Rice定理说对于程序的任何非平凡属性都是不可判定的。Rice定理我感觉是进一步扩展了停机问题,停机只是程序的一个特定属性的判定。
Rice定理是指出了程序分析的一个理论界限,实际上可以通过近似的方法来解决。近似的就要考虑的到误报和漏报,相应就是must-analysis和may-analysis。 假设正确的解是集合S,must-analysis追求的是准确,但是会给出S的子集; may-analysis追求的是全面,但是会给出S的超集。整体的衡量标准是我全都要,但是对于实际大规模分析的话,还是must-analysis比较适合。
Lattice
说到集合,就先补充一些格的知识。注意这里的格不是线性空间那个整数格,这里是偏序集。
格的定义是L = (S, ≤), ≤是集合的二元关系(包含于), 上界是⊤,下界是⊥,格中的任意两个元素都有最小上界 (x⊔y)和最大下界 和最大下界 (x⊓y),相当于集合的并和交运算。在格上的单调函数f: L → L满足如下性质
对于一个高度有限的格,单调函数f有一个最小不动点f(x)=x.
该不动点的计算过程如下
Monotone Framework
先定义Dataflow problem,有两种问题
- forward problem,从控制流的enter开始
- backward problem, 从控制流的exit开始
dataflow problem的实例包含这几个部分:
- CFG
- dataflow facts的定义域D
- 初始的dataflow fact,对于forward问题就是enter处的状态
- 交汇运算,当一个结点有多个incoming edge时,如何结合多个输入,是交还是并
- 对于CFG的每个结点n对应的dataflow function: fn : D → D ,即执行语句n的效果
must-analysis的交汇运算是交,may-analysis的交汇运算是并。 常见的fn的形式是 fn(S) = (S - KILLn) union GENn
一个具体的dataflow 例子,Forward May
\[In_s = \cup_{s\prime\in pred(s)} Out_{s\prime}\] \[Out_s = gen_s \cup (In_s - kill_s)\]第一个公式表示CFG的约束, 前置语句的输出交汇到当前语句的输入;第二个公式表示语句本身的约束。 再具体的例子就是 live variable,available expression 这些。
Solve Dataflow Equations
不动点
\[x_1 = F_1(x_1,...,x_n)\] \[x_2= F_2(x_2,...,x_n)\]把CFG的约束带入语句本身的约束,就变成上面这种形式,整体变成 F : Ln → Ln
这样一个函数,然后可以求不动点。当然这种方法的复杂度不是最好的。
MOP,LFP
- 如果f是单调的,那么
f(x ⊓ y) ≤ f(x) ⊓ f(y) - 如果f是分配的,那么
f(x ⊓ y) = f(x) ⊓ f(y)
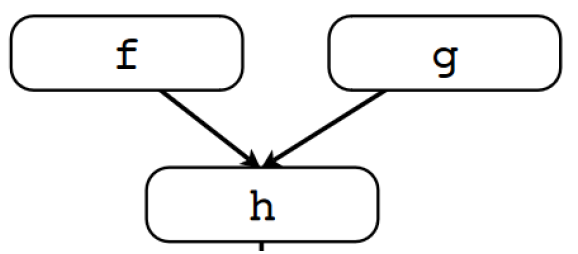
枚举所有路径,然后交汇的值
\[h(f(x)) ⊓ h(g( y)) ))\]不动点方法计算的值
\[h(f(x) ⊓ g( y))\]交汇在分配函数时,最小不动点的值(LFP)才等于meet over all path的值(MOP),否则一般是LFP<MOP
注意这里的LFP<MOP方向是和问题的交汇运算有关的, 如果是并的话就是MOP<LFP
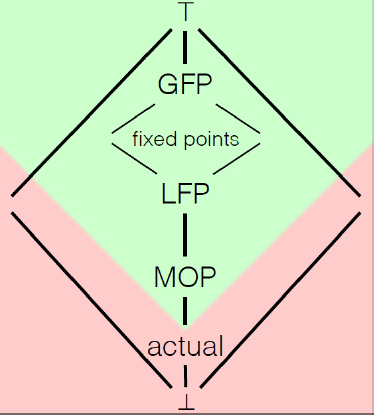
最后一张图总结
Reference
熊英飞的软件分析技术
Susan Horwitz的CS704
CMPUT 497 Foundations of Program Analysis
CS 252r: Advanced Topics in Programming Languages